Back in 2003, when I was still a player, I advocated playing against the Lucky Ladies (LL) bet. Back then, there were a few great opportunities, particularly in Washington State. In early October, 2003, I stumbled on a variation of the LL concept on the tables at the Plaza casino in downtown Las Vegas. The new side bet I observed was called “Royal 20s” (R20). The idea was similar to LL: the player was paid on any two-card 20. The main difference from LL was that there was no special payout for a pair of Queen of Hearts (with or without a dealer blackjack). The value lost from removing the top payouts from LL was given back to the player by raising the payout for an unsuited 20.
After I discovered R20, I did some AP analysis on the bet and shared my work with a couple of friends. One of them was a young card counter I had befriended a couple of months earlier. He had been having some rough days as an ordinary card counter. The fluctuations can be brutal. I told him to go to the Plaza and play against R20. He spent over a month flat betting $50 on regular blackjack and making a $50 wager on both the player and dealer sides of R20 whenever the count indicated. He e-mailed me several spread sheets showing his steady profit. Eventually he got backed off from the Plaza. Shortly after, R20 disappeared from Las Vegas. As far as I could tell, it had been burnt out and was gone. Then two days ago I read on an Internet message board that R20 had returned to Las Vegas. It was observed on a double-deck game at the Gold Coast casino in Las Vegas.
R20 pays for three different types of hands.
- The premium payout is for a “Matched 20.” This is a pair of face cards (J, Q, K) that have both the same rank and same suit. Examples include (QH,QH) and (KD,KD). Note that tens (T) are not included in the “Matched 20” payouts.
- Next, a “Suited 20” consists of two cards of the same suit whose total is 20, excluding the matched 20’s. Examples include (TH, QH), (TH, TH) and (9H, AH).
- Finally, an “Unsuited 20” is any pair of cards that sum to 20 not included as either a Matched 20 or Suited 20. Examples include (TH,QD), (TH,TD) and (9H,AD).
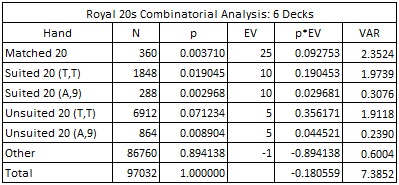
The combinatorial analysis for R20 is given below: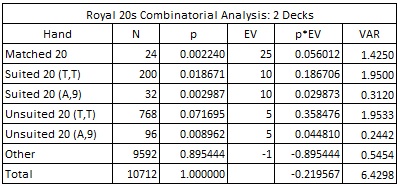
Like LL, it is obvious to the casual observer that R20 is vulnerable to card counting using the Ten Count (A = 0, 2,3,4,5,6,7,8,9 = +1, T,J,Q,K = -2), and to a lesser extent the High-Low system. In assessing this vulnerability, there are two results from the combinatorial analysis above that can be compared directly to LL.
First, in LL, the house edge for the two-deck version is 24.94% and for the six-deck version it is 24.71%. On the other hand, for R20 these edges are, respectively, 21.96% and 18.06%. It follows that the edge for the AP to overcome is significantly less; hence R20 should be more profitable for the AP.
Second, in LL, the variance for the two-deck version is 21.78 and for the six-deck version it is 24.64. For R20, these variances are, respectively, 6.43 and 7.38. In general, variance determines the overall bankroll-risk the AP assumes. In this specific situation, R20 has a significantly lower variance than LL, which means that R20 has much more appeal from a risk-aversion perspective.
With more profitability and lower variance, R20 is a much stronger opportunity for the AP to attack.
Like LL, it is not necessary to give details for the effect of removal to develop a count system. It’s clear that the AP wants to have ten-valued cards in the remainder of the shoe (T, J, Q, K) and does not want low cards (2 to 8) in the remainder of the shoe. I will first consider the double-deck game.
To get a baseline performance for a blackjack card counting system against R20, I simulated using the High-Low system (-1,1,1,1,1,1,0,0,0,-1,-1,-1,-1). I assumed a double-deck game where the cut card was placed at 75 cards (29 cards from the end). For convenience, I will refer to two decks of cards as a “shoe.”
Here are the results from a simulation of one hundred million (100,000,000) shoes of R20 using the High-Low system, with the cut card placed at 75 cards.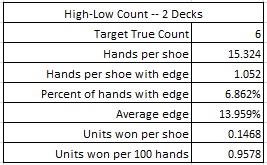
Because the AP can wager on both a “player 20” and a “dealer 20,” the AP can make two wagers whenever he has the edge. If the maximum bet is $100, and the AP is playing heads-up on a fast game, getting 200 rounds per hour, then the AP using the High-Low count will earn about $383 per hour from R20.
A more reasonable count to try is the “Ten Count,” (0,1,1,1,1,1,1,1,1,-2,-2,-2,-2). This balanced count is obviously stronger than the High-Low count. Here are the results from a simulation of one hundred million (100,000,000) shoes of R20 using this Ten Count, with the cut card placed at 75 cards.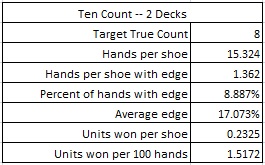
If the maximum bet is $100, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the Ten Count will earn about $607 per hour from R20. This count gives 58.4% more return than the High-Low count.
It is important for game protection to understand the extreme sensitivity of R20 to deck penetration. One of the easiest ways to protect R20 is to deal fewer cards per shoe. The following table makes this clear: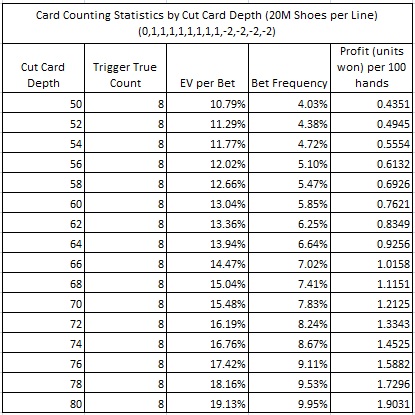
The six-deck version of R20 is far less vulnerable than the double-deck case. Here are the results from a simulation of one hundred million (100,000,000) six-deck shoes of R20 using the Ten Count, with the cut card placed at 260 cards: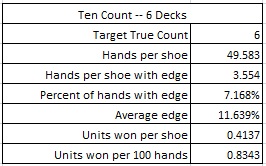
If the maximum bet is $100, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the Ten Count on a six-deck shoe game will earn about $334 per hour from R20.
Safeguarding R20 is both urgent and critical. The following are my recommendations for protecting R20:
- Watch for players who usually play R20 late in the deck at a maximum bet.
- Decreasing penetration has a strong effect in neutralizing AP opportunities. Set the shuffle point at 60 cards or less.
- Watch for the other tells of an ordinary card counter.
- In a six-deck shoe game, watch for players who play a maximum R20 bet for a certain number of hands late in the shoe and otherwise don’t play the bet.
- Consider only offering R20 from a table that uses a continuous shuffle machine.


